執筆者 : 小田 逸郎
※ 「新Linuxカーネル解読室落穂拾い」連載記事一覧はこちら
はじめに
前回は、rb-treeの紹介を始めて、挿入のアルゴリズムの説明までで終わっていました。今回は、その続きで、削除のアルゴリズムを説明します。前回を読んでいない方は、まずそちらを読んでください。前回を読まれた方ももう一度復習しておくとよいです。
red black tree (後編)
ノードの削除
ノードを削除する関数 rb_eraseのコードは以下のとおりです。(rbtree.c)
440 void rb_erase(struct rb_node *node, struct rb_root *root)
441 {
442 struct rb_node *rebalance;
443 rebalance = __rb_erase_augmented(node, root, &dummy_callbacks);
444 if (rebalance)
445 ____rb_erase_color(rebalance, root, dummy_rotate);
446 }
2段階に分かれていて、L.443の__rb_erase_augmentedでは、ノードを木から取り外します。挿入時と違うのは、取り外しには木構造の操作が必要になるということです。取り外した上で、まずは、色はそのままで木構造として正しい状態にします。そして、色に関しては、簡単に補正できるのであれば、補正を行い、問題ない場合は、NULLを返します。ノードを削除した場合、各パスの黒数が同じでなくなってしまうケースがどうしても発生し得ます(規則 5違反)。それが、rebalanceにNULLでない値が返る場合で、左右の子のパスの黒数が合わなくなってしまったノードが返されます。L.445の____rb_erase_colorでは、そのノードを起点として、各パスの黒数を合わせるべく、色の操作と木構造の操作が行われます。なお、「augmented」に関しては、本記事で取り扱いませんので、無視しておいてください*1。
ノードの取り外し
__rb_erase_augmentedのコードを見る前にどんな操作が必要か、まず説明をしておきます。削除するノードの子に着目して場合分けします。case の番号は、Linuxのコードに合わせたもので、後で参照します。
case 1
最も簡単な場合が、削除するノードに子が一つ(左右不問)だけ存在するケースです。規則 4(赤は連続しない)、規則 5(どのノードも左右の子パスの黒数は同じ)のしばりに注意しましょう。それにより、子がひとつの場合、子は必ず赤(さらには子には子はなし)、削除するノードは黒となります。
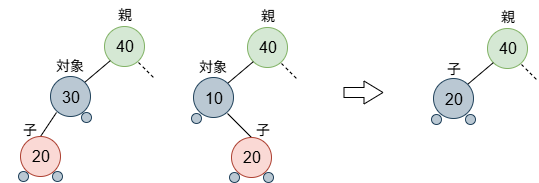
この場合、削除するノードの子をノードの位置に持っていき、色を黒に変えれば完了です。これ以上の補正は必要ないです。(なお、説明図は、削除するノードがその親の左子のケースを描いていますが、処理としては、親の右子でも変わりはありません。)
case 0
削除するノードの子がいない場合を考えます。なお、case 0というのは、分かりやすさのため、筆者が付けたもので、Linuxには出てきません。削除するノードの色は黒の場合も赤の場合もあります。
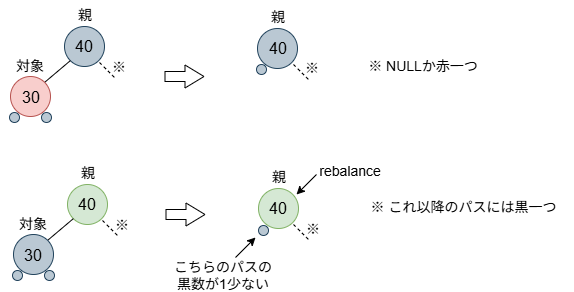
木の操作としては、単純に取り外す以外のことはやりようがないです。削除するノードが赤の場合は、簡単で、特に補正は必要ありません(図の上段)。これで、処理完了です。問題なのは、削除するノードが黒の場合で、取り外すことで、親の左右の子パスの黒数が合わなくなってしまいます(図の下段)。この場合、親ノードを補正の起点、rebalanceとして返します。(なお、説明図は、削除するノードがその親の左子のケースを描いていますが、処理としては、親の右子でも変わりはありません。)
case 2
削除するノードに左右どちらの子も存在する場合を考えます。この場合、削除するノードの次に大きいノードを削除するノードの位置に挿げ替えるという操作を行います。次に大きいノードをsuccessor(後継者)と呼びます。そこで、successorを探すことになりますが、case 2は、successorが削除するノードの直下(右子)であった場合です。
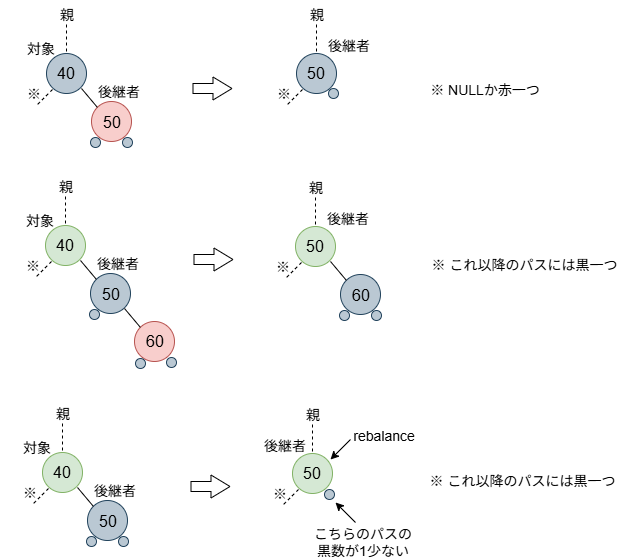
successorには、左子がいないので、successorとその右子のバリエーションは限られます。上図はそのバリエーションを網羅しています。まず、木操作としては、successorを削除するノードの位置に持っていきます。そして、色操作として、successorの色は削除するノードの色に変えます。これは、親から対象(->successorに置き換え)を経て左側(図の※方向)のパスの黒数を変えないためです。successorが赤の場合(図の上段)は、問題なしで、これで処理終了です。successorが黒の場合は、右子がいない場合(図の下段)と赤の子ひとつの場合(図の中段)があります。赤の子がいる場合は、おあつらえ向きで、その子を黒に変えれば、つじつまがあいます。それで処理終了です。問題なのは、子がいない場合で、その場合は、右側のパスの黒数が1少なくなってしまいます。successorを補正の起点、rebalanceとして返します。
case 3
successorを探す訳ですが、それには、削除するノードの右の子の左側のパスをずっと追っていくことになります。そして、左の子がNULLとなったところで、それがsuccessorとなります。
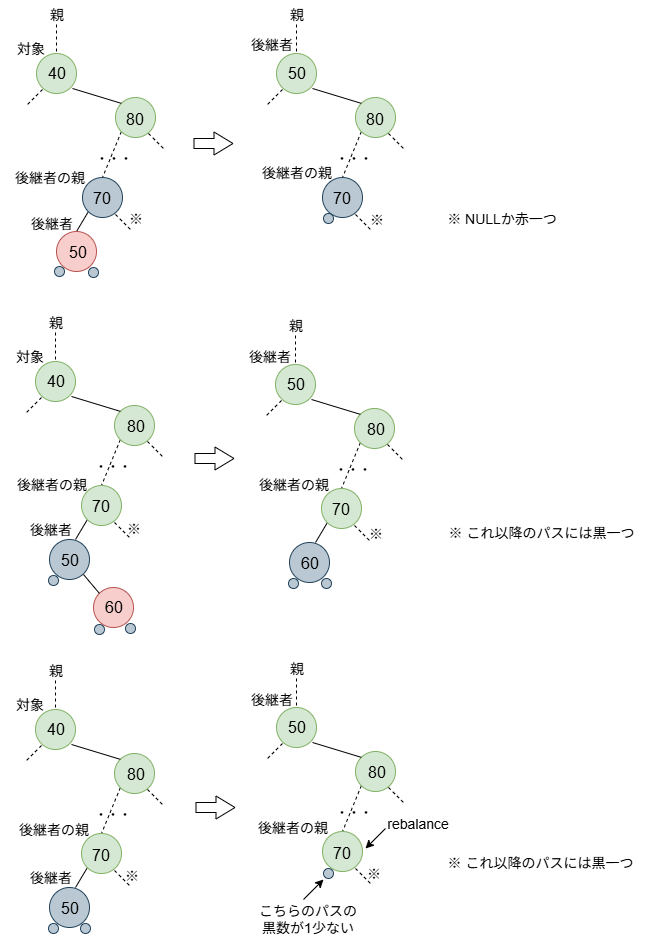
この場合もsuccessorを削除するノードの位置に挿げ替え、色は、削除するノードのものに変えます。successorとその右子のバリエーションとしては、case 2と同様で、処理も同様となります。successorが赤の場合は、問題なしです(図の上段)。successorが黒で右子がある場合(赤になる)は、successorの(元)親の左子になりますが、色を黒に変えればつじつまが合います(図の中段)。問題なのは、successorが黒で子がなかった場合で、successorの(元)親の左側の黒数が1少なくなってしまいます(図の下段)。successorの(元)親を補正の起点、rebalanceとして返します。
Linuxコード
それでは、__rb_erase_augmentedのコードを見ていきましょう。(rbtree_augmented.h)
223 static __always_inline struct rb_node *
224 __rb_erase_augmented(struct rb_node *node, struct rb_root *root,
225 const struct rb_augment_callbacks *augment)
226 {
227 struct rb_node *child = node->rb_right;
228 struct rb_node *tmp = node->rb_left;
229 struct rb_node *parent, *rebalance;
230 unsigned long pc;
231
これに限らず変数名のつけ方が分かりにくいですが、childが削除するノードの右子、tmpが削除するノードの左子です。
232 if (!tmp) {
233 /*
234 * Case 1: node to erase has no more than 1 child (easy!)
235 *
236 * Note that if there is one child it must be red due to 5)
237 * and node must be black due to 4). We adjust colors locally
238 * so as to bypass __rb_erase_color() later on.
239 */
240 pc = node->__rb_parent_color;
241 parent = __rb_parent(pc);
242 __rb_change_child(node, child, parent, root);
243 if (child) {
244 child->__rb_parent_color = pc;
245 rebalance = NULL;
246 } else
247 rebalance = __rb_is_black(pc) ? parent : NULL;
248 tmp = parent;
左子がいないケース。上で説明したcase 1とcase 0が混ざっています。L.246がcase 0の場合で、ノードが黒であれば、parentを起点にrebalanceが必要となります。L.246のelse節以外の部分は、case 1で、ノードが右子だけもつケースとなります。右子をスライドして、色を黒に変えればOKです。木操作については、L.242とL.244で行われています。色の操作は、L.244に含まれています。
249 } else if (!child) {
250 /* Still case 1, but this time the child is node->rb_left */
251 tmp->__rb_parent_color = pc = node->__rb_parent_color;
252 parent = __rb_parent(pc);
253 __rb_change_child(node, tmp, parent, root);
254 rebalance = NULL;
255 tmp = parent;
case 1で削除するノードが左子だけを持つケースです。処理については、前節と同様です。
256 } else {
257 struct rb_node *successor = child, *child2;
258
259 tmp = child->rb_left;
260 if (!tmp) {
261 /*
262 * Case 2: node's successor is its right child
263 *
264 * (n) (s)
265 * / \ / \
266 * (x) (s) -> (x) (c)
267 * \
268 * (c)
269 */
270 parent = successor;
271 child2 = successor->rb_right;
272
273 augment->copy(node, successor);
削除するノードに左右の子があった場合の処理です。L.260は、successorが削除するノードの直下(右子)だったケースです。Linuxでは、以降のcase 3とコードを共通化しており、ここでは、コードを共通化するための変数名の付け替えのみ行っています。parentがsuccessorの右子をつなぐノード、child2がそのつながれるsuccessorの右子を示しています。これに限らず、変数名の付け替えがいろいろ出てきてコードが読みづらくなっています。筆者の個人的な見解としては、コードの共通化をせず、case 2とcase 3で別々にした方が分かりやすいと思っています。
274 } else {
275 /*
276 * Case 3: node's successor is leftmost under
277 * node's right child subtree
278 *
279 * (n) (s)
280 * / \ / \
281 * (x) (y) -> (x) (y)
282 * / /
283 * (p) (p)
284 * / /
285 * (s) (c)
286 * \
287 * (c)
288 */
289 do {
290 parent = successor;
291 successor = tmp;
292 tmp = tmp->rb_left;
293 } while (tmp);
294 child2 = successor->rb_right;
295 WRITE_ONCE(parent->rb_left, child2);
296 WRITE_ONCE(successor->rb_right, child);
297 rb_set_parent(child, successor);
298
299 augment->copy(node, successor);
300 augment->propagate(parent, successor);
301 }
case 3の処理です。ここでは、successorの検索(L.289-293)と、successorの右子をsuccessorの親の左子に付け替える処理(L.294-295)を行っています。また、ノードの右子をsuccessorの右子にする処理(L296-297)も行っています。補足すると、これらは、case 2では必要ないcase 3特有の処理となります。以降は、case 2と共通コードとなります(例えば、ノードの左子をsuccessorの左子にするのは、case 2と共通)。
302
303 tmp = node->rb_left;
304 WRITE_ONCE(successor->rb_left, tmp);
305 rb_set_parent(tmp, successor);
306
307 pc = node->__rb_parent_color;
308 tmp = __rb_parent(pc);
309 __rb_change_child(node, successor, tmp, root);
310
311 if (child2) {
312 rb_set_parent_color(child2, parent, RB_BLACK);
313 rebalance = NULL;
314 } else {
315 rebalance = rb_is_black(successor) ? parent : NULL;
316 }
317 successor->__rb_parent_color = pc;
318 tmp = successor;
319 }
case 2とcase 3の続きです。ノードの左子をsuccessorの左子にする処理(L.303-305)、successorをノードの位置に挿げ替える処理(L307-309、L317)を行っています。successorの色をノードの色にする処理は、L.317に含まれます。L.311-L316は、successorの右子のバリエーションに応じた処理です。右子があれば、色を黒に変えればOK(L.312)、右子がなく、successorが黒の場合、parent(successorの元親)を起点として、rebalance必要(L.315)となります。
320 321 augment->propagate(tmp, NULL); 322 return rebalance; 323 }
augmentには触れません。rebalanceを返します。
数合わせ
____rb_erase_colorのコードを見る前にどんな操作が必要か、まず説明しておきます。操作は繰り返し行われることになりますが、操作の各ステップの開始時には前提条件があります。
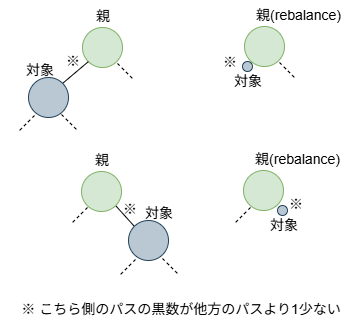
それは、対象としているノードは黒(含NULL)で、その親から見ると、ノード側のパスの黒数が他方のパスの黒数よりも1少ない状況になっているということです。__rb_erase_augmented から復帰して、____rb_erase_colorが呼び出された時点では、対象ノードは、NULLになっています(図の右側)。一番最初はその状態ですが、木構造を遡って処理が繰り返されるため、処理を考える上では、対象ノードはNULLではないし、子孫も存在している可能性があることには注意してください(図の左側)。
それでは、またケース分けをしていきましょう。その前に対象ノードは親の左子のケースを前提とします(図の上段)。右子のケース(図の下段)は例によって、「左右対称、以上お終い」となります。
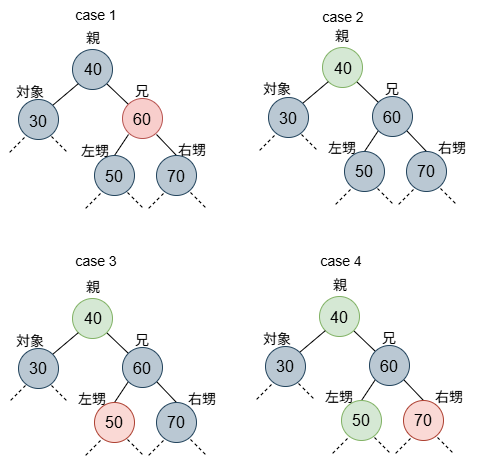
場合分けは、対象ノード(以降、単に対象)の兄弟ノード(以降、兄)の色と、兄の子の色で4とおりに分けます。case 1は兄が赤の場合で、case 2~4は兄が黒の場合です。case 2は、兄の子(以降、甥)が両方黒だった場合です。case 3は、左甥が赤、右甥が黒だった場合です。case 4は、右甥が赤だった場合で、左甥については色を問いません。場合分けとしてはすべてのケースを網羅しています。なお、子がいないケース(NULL)も黒と扱います。
case 1
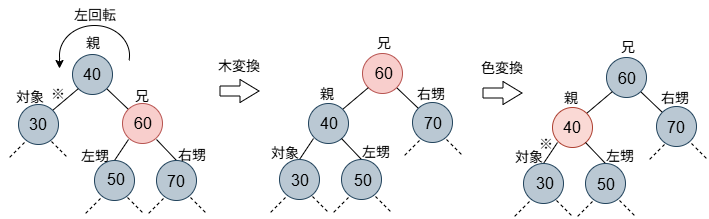
このケースでの処理は、親を対象に左回転し、親と兄の色を取り換えます。さて、変えた結果と変える前(図の左と右)を注意深く比べてみると、結局のところ、親から対象方向(図の※)の数が1少なく、その他のパスについては、数は変わらないという状況になっています。この操作は何だったかというと、対象の兄を黒にしたかったということに尽きます。対象の兄は変わりました(左甥が新たな兄)が、その状態で(対象、親は変わらず)、case 2以降の処理に進みます。ループに返るのではなく、スルーする形です。
case 2
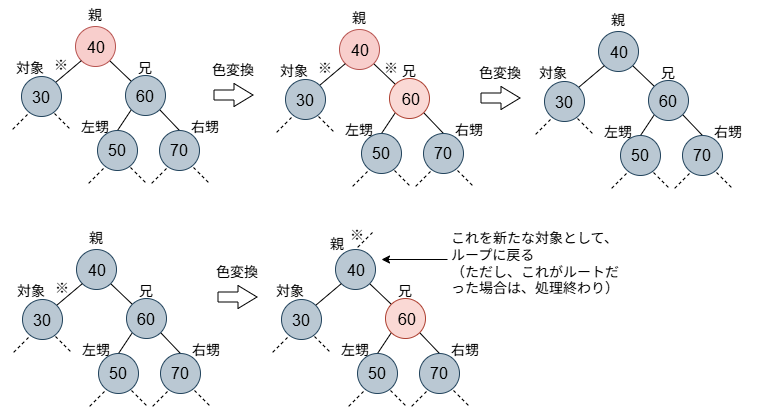
両方の甥が黒だった場合は、兄を赤に変えます。この時点で、親の左右のパスの黒数は等しく1少ない(図の※)という状況になります。親の色は、赤も黒もどちらもあり得ますが、その色により、後の処理が分かれます。親の色が赤であれば、黒に変えます(図の上段右)。そうすると、親を経由するパスの黒数は元々の数に回復していることが分かります。これにて処理は終了です。親が黒の場合(図の下段)は、親の左右のパスは等しく黒数が1少ないという状況になっています。そのため、親を新たな対象ノードとして、処理を繰り返します(ループに返ります)。ただし、親がルートであった場合は、それで処理は終了です。ノードを削除したということは、木の全体のパスの黒数が減る可能性もあるということです。途中でつじつまが合えばよいですが、処理を繰り返し、ルートまでたどり着いた、このケースが木の全体のパスの黒数が減るケースということになります。
case 3
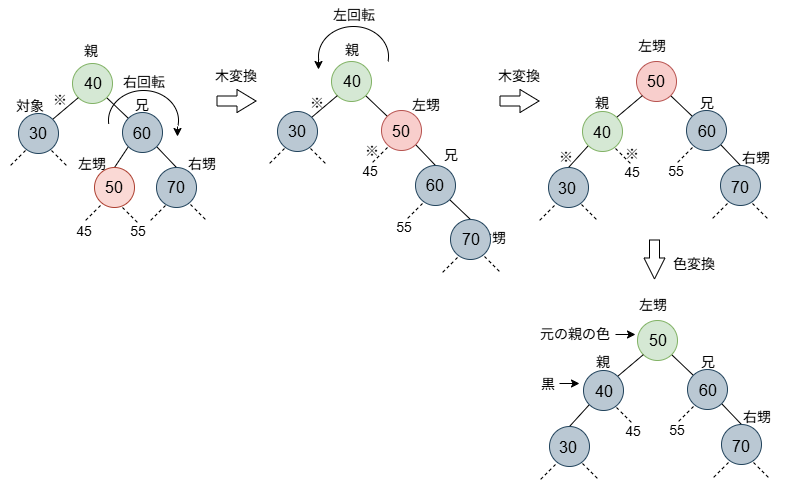
右甥が黒、左甥が赤だった場合です。この場合、結構複雑な処理となります。木の操作として、まず、兄を対象に右回転し、その後、親を対象に左回転します。色の処理としては、左甥の色を元々の親の色にし、親の色を黒にします(元々黒の場合もあり)。最終図を注意深く見てみると、図の範囲のパスの黒数がどこも1少ないパスがなく、回復していることが分かります。なお、木操作の途中では、左甥の左子(図で、45と書いたノード)のパスも黒数が1少ない状態になってしまっていますが、最終的には辻褄が合うということが裏で起こっています。case 3の場合はこれにて処理終了となります。
case 4
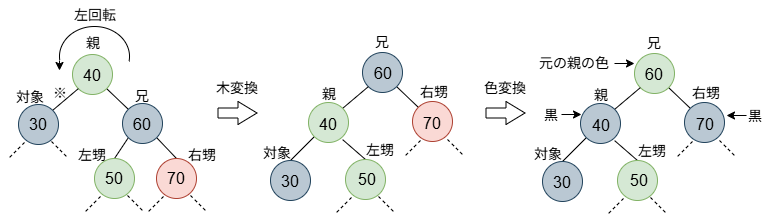
右甥が赤(、左甥の色は問わない)の場合です。木の操作として、親を対象に左回転します。色の処理として、以下の処理を行います。
- 右甥(赤)を黒に変える。
- 兄弟の色は、元々の親の色にする。(元々同じかもしれない)
- 親の色を黒にする。(元々黒かもしれない)
最終図を注意深く見てみると、対象のパスの黒数が1増えて他のパスと同じになり、他のパスは元と変わらないことが分かります。case 4の場合はこれにて終了となります。
Linuxコード
それでは、____rb_erase_colorのコードを見ていきましょう。(rbtree.c)
226 static __always_inline void
227 ____rb_erase_color(struct rb_node *parent, struct rb_root *root,
228 void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
229 {
230 struct rb_node *node = NULL, *sibling, *tmp1, *tmp2;
231
232 while (true) {
233 /*
234 * Loop invariants:
235 * - node is black (or NULL on first iteration)
236 * - node is not the root (parent is not NULL)
237 * - All leaf paths going through parent and node have a
238 * black node count that is 1 lower than other leaf paths.
239 */
最初は、対象ノードがNULLの状態からループがはじまります。ループ処理での前提条件がコメントに書いてあります。このあたり、前述で説明したとおりです。
240 sibling = parent->rb_right;
241 if (node != sibling) { /* node == parent->rb_left */
対象ノードが親の左子であるケースを考えます。siblingは、親の右子です。対象ノードの兄弟に当たります。
242 if (rb_is_red(sibling)) {
243 /*
244 * Case 1 - left rotate at parent
245 *
246 * P S
247 * / \ / \
248 * N s --> p Sr
249 * / \ / \
250 * Sl Sr N Sl
251 */
252 tmp1 = sibling->rb_left;
253 WRITE_ONCE(parent->rb_right, tmp1);
254 WRITE_ONCE(sibling->rb_left, parent);
255 rb_set_parent_color(tmp1, parent, RB_BLACK);
256 __rb_rotate_set_parents(parent, sibling, root,
257 RB_RED);
258 augment_rotate(parent, sibling);
259 sibling = tmp1;
260 }
対象ノードの兄弟が赤だったケース、すなわち、case 1です。L.252~257でやっているのは、前述の説明どおりのことです。__rb_rotate_set_parentは前回の記事を参照してください。case 1は、以降の処理に続きます。対象ノードの兄弟に当たるノードが変わっているので、変数siblingを設定し直しています(L.259)。
261 tmp1 = sibling->rb_right;
262 if (!tmp1 || rb_is_black(tmp1)) {
263 tmp2 = sibling->rb_left;
264 if (!tmp2 || rb_is_black(tmp2)) {
265 /*
266 * Case 2 - sibling color flip
267 * (p could be either color here)
268 *
269 * (p) (p)
270 * / \ / \
271 * N S --> N s
272 * / \ / \
273 * Sl Sr Sl Sr
274 *
275 * This leaves us violating 5) which
276 * can be fixed by flipping p to black
277 * if it was red, or by recursing at p.
278 * p is red when coming from Case 1.
279 */
280 rb_set_parent_color(sibling, parent,
281 RB_RED);
282 if (rb_is_red(parent))
283 rb_set_black(parent);
284 else {
285 node = parent;
286 parent = rb_parent(node);
287 if (parent)
288 continue;
289 }
290 break;
291 }
対象ノードの兄弟が黒だったケースになります。兄弟ノードの子(甥)の色での場合分けになります。L.264からは、両方の甥が黒だった場合(NULLの場合を含む)で、case 2 の処理になります。やっているのは、前述のcase 2の説明どおりのことです。兄弟の色を赤にします(L.280)。親が赤であれば、黒に変えて、終了です(L.282,283,L.290)。親が黒の場合、親を対象ノードとしてループに戻ります(L285-288)。ループに戻るのはこのケースだけになります。ただし、親がルートの場合は、終了です(L.287が偽、L.290)。
292 /* 293 * Case 3 - right rotate at sibling 294 * (p could be either color here) 295 * 296 * (p) (p) 297 * / \ / \ 298 * N S --> N sl 299 * / \ \ 300 * sl Sr S 301 * \ 302 * Sr 303 * 304 * Note: p might be red, and then both 305 * p and sl are red after rotation(which 306 * breaks property 4). This is fixed in 307 * Case 4 (in __rb_rotate_set_parents() 308 * which set sl the color of p 309 * and set p RB_BLACK) 310 * 311 * (p) (sl) 312 * / \ / \ 313 * N sl --> P S 314 * \ / \ 315 * S N Sr 316 * \ 317 * Sr 318 */ 319 tmp1 = tmp2->rb_right; 320 WRITE_ONCE(sibling->rb_left, tmp1); 321 WRITE_ONCE(tmp2->rb_right, sibling); 322 WRITE_ONCE(parent->rb_right, tmp2); 323 if (tmp1) 324 rb_set_parent_color(tmp1, sibling, 325 RB_BLACK); 326 augment_rotate(sibling, tmp2); 327 tmp1 = sibling; 328 sibling = tmp2; 329 }
右甥が黒、左甥が赤だったケースです。case 3のケースになります。ここでやっているのは、前述のcase 3の説明のうち、第1段階の回転操作のみです。Linuxのコードでは、case 3の第2段階の回転操作以降は、case 4のコードと共通化しています。上記のコメントには、case 4の処理でどうなるかご丁寧に示してくれています。しかしながら、わざわざコードを共通化せず、case 3とcase 4で完全にコードを分けて書いた方が分かりやすいと思います(コードを共通化できるかもしれませんが、説明図を見てもらえば分かるようにcase 3の第1段階後とcase 4は、まったく同じ状態ではありません)。最後にcase 4の処理と合流するための変数名の付け替えを行っています(L.327,328)。case 4での右甥(tmp1)に当たるものが、case 3(の第1段階後)での兄弟(sibling)となります(L.327)。case 4での兄弟ノード(sibling)に当たるものがcase 3(の第1段階後)での左甥(tmp2)となります(L.328)。
330 /* 331 * Case 4 - left rotate at parent + color flips 332 * (p and sl could be either color here. 333 * After rotation, p becomes black, s acquires 334 * p's color, and sl keeps its color) 335 * 336 * (p) (s) 337 * / \ / \ 338 * N S --> P Sr 339 * / \ / \ 340 * (sl) sr N (sl) 341 */ 342 tmp2 = sibling->rb_left; 343 WRITE_ONCE(parent->rb_right, tmp2); 344 WRITE_ONCE(sibling->rb_left, parent); 345 rb_set_parent_color(tmp1, sibling, RB_BLACK); 346 if (tmp2) 347 rb_set_parent(tmp2, parent); 348 __rb_rotate_set_parents(parent, sibling, root, 349 RB_BLACK); 350 augment_rotate(parent, sibling); 351 break;
右甥が赤(左甥の色は問わない)のケースで、case 4に当たります。この部分のコードは、case 3の続きとしても使用されていますが、まずは、この部分をcase 4の場合だけとして、前述のcase 4の説明どおりの処理になっているかを確認し、その後、case 3の続きであるとして読んで、case 3の説明の続きとしても成り立っていることを確認するとよいかと思います。L.342-349は、確かにcase 4の説明にある、親を対象とした左回転および、説明にある色操作をしているのと同じです。case 3の続きとして見た場合にも一応成立していることが確認できます。が、そういう確認をすること自体が面倒ですし、繰り返しになりますが、case 3とcase 4のコードを分けた方が分かりやすいです。case 3、case 4とも問題は解消されたので、処理は終わりです(L.351)。
352 } else {
353 sibling = parent->rb_left;
354 if (rb_is_red(sibling)) {
355 /* Case 1 - right rotate at parent */
356 tmp1 = sibling->rb_right;
357 WRITE_ONCE(parent->rb_left, tmp1);
358 WRITE_ONCE(sibling->rb_right, parent);
359 rb_set_parent_color(tmp1, parent, RB_BLACK);
360 __rb_rotate_set_parents(parent, sibling, root,
361 RB_RED);
362 augment_rotate(parent, sibling);
363 sibling = tmp1;
364 }
365 tmp1 = sibling->rb_left;
366 if (!tmp1 || rb_is_black(tmp1)) {
367 tmp2 = sibling->rb_right;
368 if (!tmp2 || rb_is_black(tmp2)) {
369 /* Case 2 - sibling color flip */
370 rb_set_parent_color(sibling, parent,
371 RB_RED);
372 if (rb_is_red(parent))
373 rb_set_black(parent);
374 else {
375 node = parent;
376 parent = rb_parent(node);
377 if (parent)
378 continue;
379 }
380 break;
381 }
382 /* Case 3 - left rotate at sibling */
383 tmp1 = tmp2->rb_left;
384 WRITE_ONCE(sibling->rb_right, tmp1);
385 WRITE_ONCE(tmp2->rb_left, sibling);
386 WRITE_ONCE(parent->rb_left, tmp2);
387 if (tmp1)
388 rb_set_parent_color(tmp1, sibling,
389 RB_BLACK);
390 augment_rotate(sibling, tmp2);
391 tmp1 = sibling;
392 sibling = tmp2;
393 }
394 /* Case 4 - right rotate at parent + color flips */
395 tmp2 = sibling->rb_right;
396 WRITE_ONCE(parent->rb_left, tmp2);
397 WRITE_ONCE(sibling->rb_right, parent);
398 rb_set_parent_color(tmp1, sibling, RB_BLACK);
399 if (tmp2)
400 rb_set_parent(tmp2, parent);
401 __rb_rotate_set_parents(parent, sibling, root,
402 RB_BLACK);
403 augment_rotate(parent, sibling);
404 break;
405 }
406 }
407 }
L.352以降は、対象ノードが親の右子だったケースです。これは、対象ノードが親の左子だったケース(L.241-351)と左右対称です。コードもコピペして、「right」と「left」を相互変換しただけであり、処理としてもそれで正しいです。説明は割愛します。
あとがき
前回と今回で、Linuxのrb-treeの実装について、皆さんが興味がありそうな挿入と削除のアルゴリズムを紹介しました。赤と黒の色分けをすることで巧妙にバランスを取っているのが分かったかと思います。挿入したときは、どこかの赤を黒に、削除したときは、どこかの黒を赤に変えることで、局所的に辻褄を合わせられるのではないか、というのが基本的なアイデアかと思います。局所的にうまくいかなければ、段々ルートに遡って、ルートまで辿り着いたときは、全体の数が1変わるというわけです。これまでの説明は、どういう配置のときにどの色を変えればよいか、回転によりその配置にできるのはどのパターンか、というレシピであると言えます。最初にこのレシピを考えた人はえらいと思います。
さて、rb-treeの実装を調べるにあたり、web上のいろいろな記事を見てみましたが、よく理解できませんでした。しかしながら、自分が理解してしまった上で、読んでみると書いてあることが分かります。分かっていると分かるけど、分かるためには使えないというわけで、なかなか難しいものです。この記事もそうなっていないか心配ではありますが、少しでも皆さんの理解の助けになれば幸いです。
こういったものの理解には、自分でプログラムを書いてみるのが早道でもあります。補足資料に筆者がpythonで書いた、rb-treeの実装があるので、それも参考にしてください。Linuxのコードの分かりにくい部分を改善し、かなり分かりやすくなっているかと思います(筆者比)。
OSとしては、rb-treeを使う立場であって、使い方と使いどころが分かっていれば、実装を知らなくても困りません。しかしながら、OSなどをやっている人種は、実装を知らないともやもやして、気になってしまう人種ですもんね。そのもやもやを解消する参考としてください。今回無視したaugmentは、rb-treeの実装を知らないと理解は難しいですが、rb-treeの実装を理解してしまえば、理解は難しくありません。興味のある方は自力で調べてみてください。
次回以降は、また、何かを拾っていこうと思います。お楽しみに。
*1:拾うのであれば、また別の機会ということで。