執筆者 : 小田 逸郎
※ 「新Linuxカーネル解読室落穂拾い」連載記事一覧はこちら
はじめに
前回は、基本的な管理構造である、リンクリストについて、説明しました。大昔のOSでは、リンクリストぐらいで事足りていたのですが、今では、管理するリソースの数が膨大なため、それだけでは足りなくなってきました。そこで、今回は、リンクリストよりは複雑で、Linuxで結構よく使われている構造である、red black tree(以降、rb-tree) を紹介します。rb-tree自体は、特に新しいものではありません。旧解読室の頃には既に使われていました。ただし、旧解読室にはキーワードは出てきました*1が、解説はありませんでした。rb-treeはリソースを管理する構造というだけで、OSの本質的な処理を学ぶためには、その実装を理解する必要はなく、部品として使用できれば十分であるとは言えます。とは言え、さも当然のように「rb-treeに挿入も行っています」*2などと使われている一方で、rb-treeの解説はどこにもないという状況には、少しもやもやした気分になりますよね。ということで(今更ながらですが)、このブログで拾っていこうと思います。
red black tree (前編)
rb-treeとは
そもそもrb-treeとはどんなものかというと、ざっくりと言ってしまえば、2分木の一種です。2分木というのは、ルート(根)を頂点として、左右の枝を持つノードで連結した構造で、ルートからキーの大小比較を行いながら下に辿っていき、目的のキーを持つノードを見つけることができるというものです。

キーとして整数を使用した例です。どちらも構造としては正しいですが、右のものは、いかにもバランスが悪いです。左の例のようにバランスが良くないと検索の効率が良くなりません。rb-treeというのは、バランスを保つように工夫をした2分木で、特徴としては、ノードを赤と黒の2種類の色で分けていることです。それがそのまま名前の由来になっています。
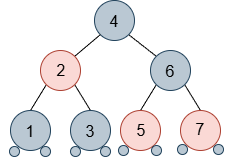
rb-treeには5つの規則があります。
- 規則 1: ノードは赤か黒
- 規則 2: ルートは黒
- 規則 3: 終端(NULL)は黒(扱い)
補足: 各パスの黒の数を揃えることになりますが、NULLについては実際のところ勘定に入れる必要はないです。木の操作を考える場合、NULLを黒とみなすと都合がよいです。図では、小さな黒丸で表しています。 - 規則 4: 赤の子は黒
補足: 黒は連続してもよいが、赤が連続するのはだめということ。 - 規則 5: ルートから終端に至るどのパス上も黒の数は同じ
規則4と規則5から、黒ノードだけからなるパスが一番短く、黒と赤が交互になっているパスが一番長くなるので、最も長いパスは最も短いパスの最悪2倍ということになります。ですので完全にバランスしているわけでないけど、そこそこバランスしていると言えます。上記の規則があるおかげで、バランスを取るための操作がやりやすくなっているのがポイントでもあります(言うても、「比較的には」ではありますが)。
リンクリストでは、検索のためのコストが要素数(n)に対して線形のオーダ(O(n))ですが、rb-treeでは、log(n)のオーダ(O(log(n))なので、要素数が多くなると効果が高いと言えます。
Linuxのrb-tree実装
Linuxのrb-treeの実装に関わるファイルは以下のとおりです。本記事では、この中から一部を取り上げて、実装を解説します。
- include/linux/rbtree_types.h
rb-treeの構造体定義(ex. rb_node) - include/linux/rbtree.h
rb-treeのAPI定義。rb-treeを使いたい人は、これをincludeする。 - include/linux/rbtree_augmented.h
augmentedに関しては、本記事では取り上げない。rb-tree内部の実装に関してはaugmentedを考慮した実装になっている。 - lib/rbtree.c
rb-treeの実装本体。とは言え、ヘッダ(rbtree.h、rbtree_augmented.h)にも実装コードは多い。
rb-treeを構成するための構造体は以下の2つです(rbtree_types.h)。
struct rb_node {
unsigned long __rb_parent_color;
struct rb_node *rb_right;
struct rb_node *rb_left;
};
struct rb_root {
struct rb_node *rb_node;
};
rb_nodeがノードを表す構造体、rb_rootがルートをポイントするための構造体です。rb_nodeのメンバ rb_right、rb_leftはそれぞれ、右の子ノードと左の子ノードをポイントするものですが、__rb_parent_colorという変わったメンバがあります。これは、親へのポインタとノード自身の色を一つのunsigned long 変数に押し込めたものとなります。色の定義は以下のとおりです(rbtree_augmented.h)。
#define RB_RED 0 #define RB_BLACK 1
ポインタの下位数ビットは0であることが保証されているので、その下位1ビットを色を表すために使用しています。rb_nodeは、本来、自然に定義するなら以下のようになるでしょう(rb_node自然版)。
struct rb_node {
int rb_color; /* RB_RED or RB_BLACK */
struct rb_node *rb_parent;
struct rb_node *rb_right;
struct rb_node *rb_left;
};
__rb_parent_color は、「(unsigned long)rb_parent | rb_color」としたものになります。これは、メモリを節約する目的で、まあよくあるテクニックではあります。1ビットで済むところを数バイト使うというのは勿体ないといえば勿体ないですが、筆者は全くお勧めしません。というのは、これによりコードが煩雑で読みづらくなるためで、実際、Linuxのコードは、結構分かりづらくなっています。そのままポインタとしてアクセスしてしまうバグも容易に想像でき、コードレビューにも無駄に注意が必要になってしまいます。最近はメモリも潤沢ですし、コードの読みやすさやメンテナンスしやすさを重視すべきだと考えています。本当にこれがリソースや性能上クリティカルだと分かるまでは、考えなくて良いです。
rb_nodeは、木構造を構成するのに必要な部分だけで、キーについては、何も関知していません。rb_nodeは、通常、rb-treeを使用したい人が管理する構造体に埋め込まれて使用されることになります。
struct hoge {
struct rb_node hoge_rb_node;
...
int hoge_key; /* 何らかのキー。型はintである必要はなく、何でもよい。*/
};
今ではお馴染みになった、container_of() を使って、rb_nodeから、それを含んでいる構造体を得ることになります。rb-treeを使用する代表的なAPIを以下に示します(rbtree.h、rbtree.c)。
struct rb_node *rb_find(const void *key, const struct rb_root *tree,
int (*cmp)(const void *key, const struct rb_node *));
void rb_add(struct rb_node *node, struct rb_root *tree,
bool (*less)(struct rb_node *, const struct rb_node *));
void rb_erase(struct rb_node *node, struct rb_root *root)
rb_findは、指定したkeyと等しいノードを検索します。keyが実際どんなものかは、使用者の自由で、rb_findには、使用者が定義した比較関数(cmp)を指定します。cmpの仕様は、以下のとおりです。
- key が ノードのkey よりも小さければ、-1 を返す。
- key が ノードのkey と等しければ、0 を返す。
- key が ノードのkey よりも大きければ、1 を返す。
前述のstruct hogeを例に取ると、以下のような関数を用意することになります。
int hoge_cmp(const void *key, const struct rb_node *node)
{
struct hoge *hp = container_of(node, struct hoge, hoge_rb_node);
if ((int)key < hp->hoge_key) {
return -1;
} else if ((int)key > hp->hoge_key) {
return 1;
}
return 0;
}
rb_addは、木に新しいノードを追加します。指定する関数lessは、追加しようとするノードのkeyが小さいかどうかを返す関数です。第一引数が追加するノード、第二引数が比較対象となる木の既存ノードになります。ここで比較するのは小さいかどうかということに注意してください。どういうことかというと、Linuxのrb-treeは、keyの重複を許しています。keyの重複があった場合、rb_findで返るのは、どうなるかと言うと、それは等しいkeyを持つノードのうち、どれが返るかは分からないということです。まあ、どれが返っても問題ない場合はそれでも良いということですね。通常は、管理するデータのkeyに重複があるとしても、ノードで取り扱うkeyには重複はないようにしておき、ノード内で重複したkeyのデータをリンクリストで管理するなどの構造を取ることを考えそうな気がします。以降の説明では、分かりやすさのため、keyに重複はないものとします。
rb_eraseは、指定したノードを木から削除します。
木の操作
さて、一番知りたいのは、ノードの挿入や削除のときのアルゴリズムはどうなっているかでしょう。その説明に行く前に木の操作で良く出てくるパターンについて触れておきます。
最初は、親につながるノードを取り換える操作です。(同等のコードが、rbtree_augmented.hにあります。)
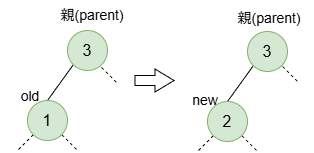
void _rb_change_child(struct rb_node *old, struct rb_node *new,
struct rb_node *parent, struct rb_root *root)
{
if (parent) {
if (parent->rb_left == old)
parent->rb_left = new;
else
parent->rb_right = new;
} else
root->rb_node = new;
}
図では、親の左子の取り換えの例になっていますが、親の右子の取り換えもできます。また、old/newがルートのケース(すなわち、parentがNULLのケース)も考慮されています。そのため、引数にrootが必要な訳です。
なお、本ブログの図では、色が赤か黒か不問の場合は、上図のように緑で表すことにします。また、木の操作のイメージが付きやすいように、具体的な数字例を入れていきます。
次は回転操作です。左回転と右回転があります。まずは左回転です。
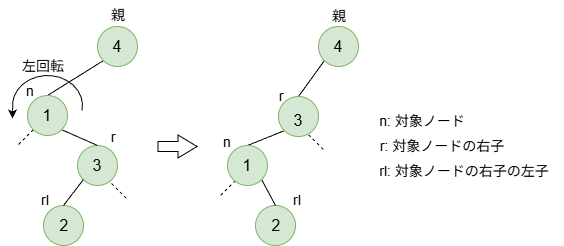
図のnodeとnodeの右子を入れ替える操作です。nodeを中心に見て、左に回転しているイメージとなります。コードにすると以下のようになります。(分かりやすさのため、rb_node自然版を使用)
void _rb_rotate_left(struct rb_node *node, struct rb_root *root)
{
struct rb_node *n, *r, *p, *rl;
n = node;
r = node->rb_right; # must not be None
p = node->rb_parent;
rl = r->rb_left;
r->rb_parent = p;
n->rb_parent = r;
n->rb_right = rl;
if (rl != NULL) {
rl->rb_parent = n;
r->rb_left = n;
}
_rb_change_child(n, r, p, root);
}
次に右回転です。
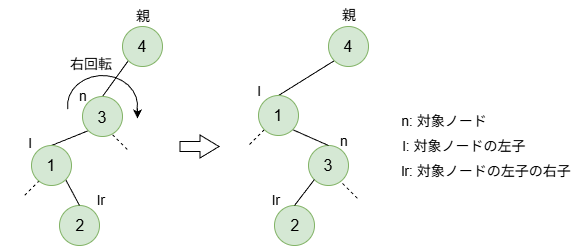
図のnodeとnodeの左子を入れ替える操作です。nodeを中心に見て、右に回転しているイメージとなります。コードにすると以下のようになります。
void _rb_rotate_right(struct rb_node *node, struct rb_root *root)
{
struct rb_node *n, *l, *p, *lr;
n = node;
l = node->rb_left; # must not be None
p = node->rb_parent;
lr = l->rb_right;
l->rb_parent = p;
n->rb_parent = l;
n->rb_left = lr;
if (lr != NULL) {
lr->rb_parent = n;
l->rb_right = n;
}
_rb_change_child(n, l, p, root);
}
左回転と右回転は左右対称になります。このコードと前のコードを注意深く見比べてみると、下のコードは上のコードをコピペして、right(r)とleft(l)を取り換えただけということが分かります。このパターンは後でも出てきます。
ここでの回転操作は、単に構造の変換だけで、色の処理は含んでいません。Linuxでは、回転操作に関して、コメント中での言及はありますが、対応するコードはありません。ないのは、__rb_parent_colorの導入の弊害だと思いますが、説明としてはあった方が分かりやすいので、使って行きます。
ノードの挿入
これからは、Linuxのコードも参照して解説していきます。バージョンとしては、6.17.1 を使用しており、付いている行番号はそのバージョンのものとなります。このあたりのコードは、あまり変わることはないかと思いますが、ここでの行番号はあくまでも記事中での参照のためのものです。
ノードを挿入する関数 rb_addのコードは以下のとおりです。(rbtree.h)
194 static __always_inline void
195 rb_add(struct rb_node *node, struct rb_root *tree,
196 bool (*less)(struct rb_node *, const struct rb_node *))
197 {
198 struct rb_node **link = &tree->rb_node;
199 struct rb_node *parent = NULL;
200
201 while (*link) {
202 parent = *link;
203 if (less(node, parent))
204 link = &parent->rb_left;
205 else
206 link = &parent->rb_right;
207 }
208
209 rb_link_node(node, parent, link);
210 rb_insert_color(node, tree);
211 }
nodeを含む構造体(特にキー)は既に設定されている必要があります。L.201~207は、nodeをつなぐ場所(link)をless関数を使用して探しているところです。つなぐ場所(link)が分かったら、L.209のrb_link_nodeで実際につなぎます。rb_link_nodeのコードは以下のとおりです。(rbtree.h)
59 static inline void rb_link_node(struct rb_node *node, struct rb_node *parent,
60 struct rb_node **rb_link)
61 {
62 node->__rb_parent_color = (unsigned long)parent;
63 node->rb_left = node->rb_right = NULL;
64
65 *rb_link = node;
66 }
L.62、63でrb_nodeの各メンバを初期化してますが、注意すべきなのは、新規に挿入するノードの色は赤だということです。L.65で実際に木に接続します。
新規のノードを木に接続しましたが、ここで注意すべきは、rb-treeの規則に反しているかもしれないということです。
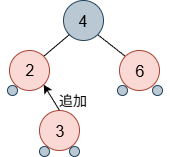
上の図では、新規に追加した部分が赤の連続になっており、規則4に反しています。L.210のrb_insert_color関数は、規則に合致するよう、ノードの色や木の構成を変えることを行っています。
rb_insert_colorのコードを見る前に、どういった操作が必要なのか整理しておきましょう。
まず、最初にひとつ目のノードを木に追加する場合、それがルートになりますが、赤のため規則2に反しますので、黒に変えます。それでOKです。最も簡単なのは、追加したノードの親が黒だった場合で、その場合は、何の規則にも反しません。よって、何もする必要がありません。
問題なのは、親が赤だった場合です。その場合、赤が連続してしまい、規則4に反するので、何らかの対処が必要となります。
対処に関しては、追加したノードの伯父に当たるノードの色と追加したノードと親の位置関係により、3つのケースに分かれます。ここでは、親は祖父の左子、伯父は、祖父の右子である場合を考えます。なお、親が赤なので、祖父は存在します。
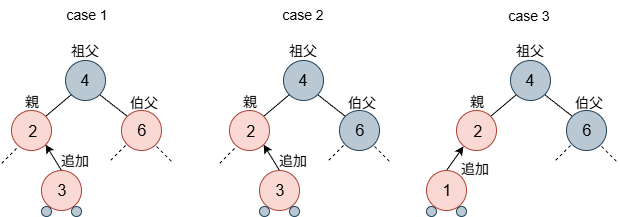
case 1は、伯父が赤だったケースです。追加ノードは、親の右子でも左子でもどちらでもよいです。case 2とcase 3は、伯父が黒だったケースです。case 2は、追加ノードが親の右子だった場合、case 3は、追加ノードが親の左子だった場合です。なお、伯父がいない場合は、黒の扱いです(規則 3)。
caseの番号付けは、Linuxのコードに合わせたもので、後でコードを見るときに参照します。説明としては、1、3、2の順でします。
case 1
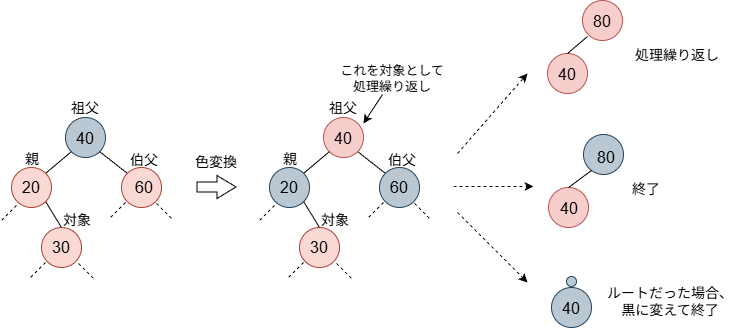
case 1では、祖父、親、伯父の色を反転させます。すなわち、祖父を黒->赤、親と伯父を赤->黒とします。部分的に見ると、赤の連続(規則 4違反)もなくなり、各パスの黒数も以前と同じで問題ありません。しかしながら、赤に変えた祖父の親が赤かもしれませんので、実は問題を先送りしていることになります。祖父を追加したノードとみなし、もう一度、対処をやり直す必要があります。このように、case 1は単独では完結せず、処理を繰り返すことになります。
case 1の後としては、祖父の親が黒で結局問題なかった場合もあれば、後に示す、case 2やcase 3の処理が実施される場合もあり、様々です。もし、case 1を繰り返しながら、ルートまでたどり着いてしまった場合、すなわち、ルートが赤になってしまった場合は、黒に変えて終了です。このケースが全体の黒数が1増えるケースとなります(図の右側下段)。
case 1の後に処理が繰り返されることから、処理を見ていく上で、追加したノードの子孫もあるかもしれないことには注意が必要です。図ではそれを表現するため、点線を入れています。図の追加ノード(30)が処理の最初であれば、子はNULLですが、繰り返し処理の過程のものであれば、子孫があることになります。
case 3
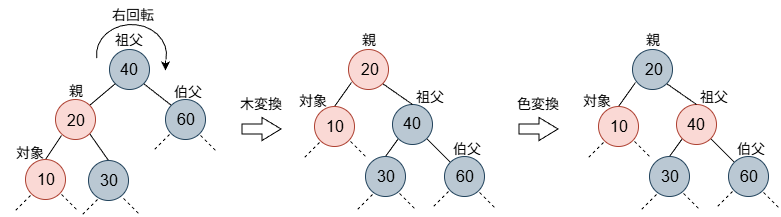
case 3では、まず、祖父を対象に右回転し、以下の色操作を行います。
- (祖父の位置になった)親の色を元々の祖父の色にする。(すなわち、赤->黒)
- (伯父の位置になった)祖父の色を赤にする。(すなわち、黒->赤)
変換後は、赤の連続(規則 4違反)がなくなり、パス上の黒数も変換前と違っていない、すなわち問題ないことが分かります。
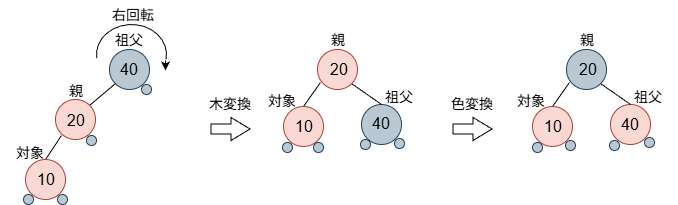
伯父がいないケースも上図に示しておきます。黒数の制約から、上図のパターンしかありません。この場合もうまく行っていることを確認できます。
case 2
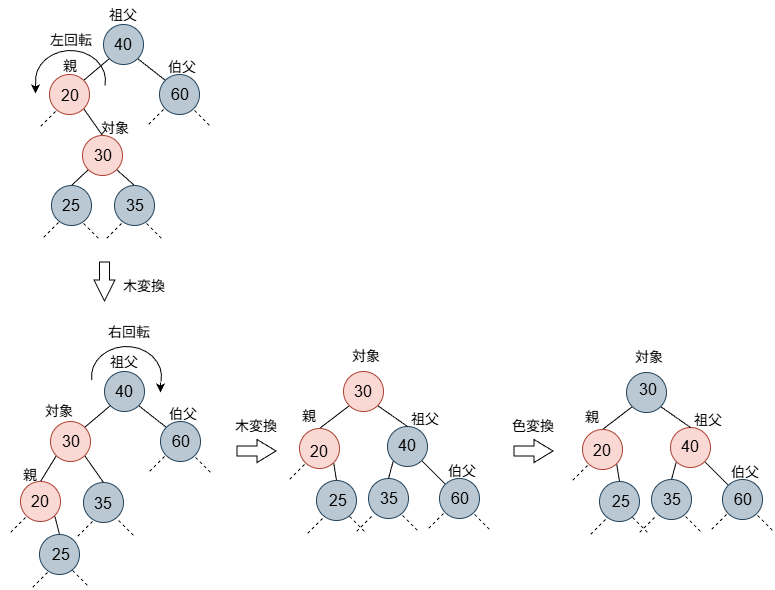
case 2では、まず、親を対象に左回転します。そうすると、親と追加ノードの立場が逆ではありますが、case 3の状態になります。そこで、親と追加ノードの立場を変えて、case 3と同じ処理を行います。
case 3の位置関係が重要ということですね。上の図で、ノード(35)の位置に来るものが黒になるようにする必要があり、それには、case 3の配置が必要ということです。
叔父パターン
親が祖父の右の子、すなわち、叔父が祖父の左の子であった場合は、前述の処理と全く左右対称の処理を行えばよいことになります。
Linuxコード
それでは、いよいよ、rb_insert_colorの処理に行きますが、最終的に実行される本体は、__rb_insert(rbtree.c)になります。
84 static __always_inline void
85 __rb_insert(struct rb_node *node, struct rb_root *root,
86 void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
87 {
88 struct rb_node *parent = rb_red_parent(node), *gparent, *tmp;
89
90 while (true) {
91 /*
92 * Loop invariant: node is red.
93 */
case 1で処理の繰り返しになるため、全体として1つのwhileループになっています。nodeが追加したノードにあたる処理対象で、ループの不変条件としては、nodeが赤であることです。
94 if (unlikely(!parent)) {
95 /*
96 * The inserted node is root. Either this is the
97 * first node, or we recursed at Case 1 below and
98 * are no longer violating 4).
99 */
100 rb_set_parent_color(node, NULL, RB_BLACK);
101 break;
102 }
nodeの親がいなかった場合です。nodeが木の最初のノードであった場合か、処理の繰り返しでルートまでたどり着いた場合です。nodeを黒に変えて終了です。
103 104 /* 105 * If there is a black parent, we are done. 106 * Otherwise, take some corrective action as, 107 * per 4), we don't want a red root or two 108 * consecutive red nodes. 109 */ 110 if(rb_is_black(parent)) 111 break;
親が黒だった場合は、これで問題解決です。初めから、追加したノードの親が黒だった場合もあれば、case 1を繰り返して、ここに到達した場合もあります。
112
113 gparent = rb_red_parent(parent);
114
115 tmp = gparent->rb_right;
116 if (parent != tmp) { /* parent == gparent->rb_left */
親(parent)が赤なので祖父(gparent)はいます。rb_red_parentは、ノードが赤だと確定している場合に親ポインタを取得する関数です。要するにマスク取る処理を省略する目的のものです。L.116から、親が祖父の左の子の場合の処理を進めます。
117 if (tmp && rb_is_red(tmp)) {
118 /*
119 * Case 1 - node's uncle is red (color flips).
120 *
121 * G g
122 * / \ / \
123 * p u --> P U
124 * / /
125 * n n
126 *
127 * However, since g's parent might be red, and
128 * 4) does not allow this, we need to recurse
129 * at g.
130 */
131 rb_set_parent_color(tmp, gparent, RB_BLACK);
132 rb_set_parent_color(parent, gparent, RB_BLACK);
133 node = gparent;
134 parent = rb_parent(node);
135 rb_set_parent_color(node, parent, RB_RED);
136 continue;
137 }
伯父が赤だった場合、すなわち、case 1です。先ほど説明した処理を行っているのが確認できます。rb_set_parent_color は、親ポインタと色から、__rb_parent_color に設定する関数です。L.134で、処理対象(node)を祖父(gparen)に置き換え、ループの最初に戻ります(L.136)。
以下、伯父が黒だった場合となります。
138
139 tmp = parent->rb_right;
140 if (node == tmp) {
141 /*
142 * Case 2 - node's uncle is black and node is
143 * the parent's right child (left rotate at parent).
144 *
145 * G G
146 * / \ / \
147 * p U --> n U
148 * \ /
149 * n p
150 *
151 * This still leaves us in violation of 4), the
152 * continuation into Case 3 will fix that.
153 */
154 tmp = node->rb_left;
155 WRITE_ONCE(parent->rb_right, tmp);
156 WRITE_ONCE(node->rb_left, parent);
157 if (tmp)
158 rb_set_parent_color(tmp, parent,
159 RB_BLACK);
160 rb_set_parent_color(parent, node, RB_RED);
161 augment_rotate(parent, node);
162 parent = node;
163 tmp = node->rb_right;
164 }
L.140のif文は、対象ノードが親の右の子だった場合で、case 2の場合となります。このif文で行っているのは、前述の説明の第一段階だけです。以降は、case 3と同じ操作となるため、変数名を以降で行うcase 3の処理に合わせるために変更しています。親(parent)の立場にnode、親の右子(tmp)の立場にnodeの右の子がなります(L.162、163)。なお、nodeの立場にparentがなりますが、case 3では、nodeの処理がないため、変数の取り換えはしていません。ここで行っているのは木構造の変更だけで、色の処理はしていません。L.159、160で色が出てきますが、これは元の色です。親ポインタと色を合体したせいで、分かりづらくなっています。
165 166 /* 167 * Case 3 - node's uncle is black and node is 168 * the parent's left child (right rotate at gparent). 169 * 170 * G P 171 * / \ / \ 172 * p U --> n g 173 * / \ 174 * n U 175 */ 176 WRITE_ONCE(gparent->rb_left, tmp); /* == parent->rb_right */ 177 WRITE_ONCE(parent->rb_right, gparent); 178 if (tmp) 179 rb_set_parent_color(tmp, gparent, RB_BLACK); 180 __rb_rotate_set_parents(gparent, parent, root, RB_RED); 181 augment_rotate(gparent, parent); 182 break;
case 3の処理です。case 2の2段階目以降もここに合流します。注意深く読むと行っているのは、前述のcase 3の説明で行っていることと同じです。__rb_rotate_set_parentsのコードは以下のとおりです。
74 static inline void
75 __rb_rotate_set_parents(struct rb_node *old, struct rb_node *new,
76 struct rb_root *root, int color)
77 {
78 struct rb_node *parent = rb_parent(old);
79 new->__rb_parent_color = old->__rb_parent_color;
80 rb_set_parent_color(old, new, color);
81 __rb_change_child(old, new, parent, root);
82 }
oldとnewの位置を交換し、newの色は、元々のoldに色とし、oldの色は、指定したcolorにするというものです。ちょっとしたヘルパー関数です。本来、回転操作を関数とし、回転操作をした後に色操作をする方がずっと簡単なのですが、親ポインタと色を合体したせいで、こんな中途半端な関数しか用意できていないです。
case 2、3 に関しては、これで問題解決なので、ループを抜けます(L.182)(ループ抜けた後は、returnするだけ)。
183 } else {
184 tmp = gparent->rb_left;
185 if (tmp && rb_is_red(tmp)) {
186 /* Case 1 - color flips */
187 rb_set_parent_color(tmp, gparent, RB_BLACK);
188 rb_set_parent_color(parent, gparent, RB_BLACK);
189 node = gparent;
190 parent = rb_parent(node);
191 rb_set_parent_color(node, parent, RB_RED);
192 continue;
193 }
194
195 tmp = parent->rb_left;
196 if (node == tmp) {
197 /* Case 2 - right rotate at parent */
198 tmp = node->rb_right;
199 WRITE_ONCE(parent->rb_left, tmp);
200 WRITE_ONCE(node->rb_right, parent);
201 if (tmp)
202 rb_set_parent_color(tmp, parent,
203 RB_BLACK);
204 rb_set_parent_color(parent, node, RB_RED);
205 augment_rotate(parent, node);
206 parent = node;
207 tmp = node->rb_left;
208 }
209
210 /* Case 3 - left rotate at gparent */
211 WRITE_ONCE(gparent->rb_right, tmp); /* == parent->rb_left */
212 WRITE_ONCE(parent->rb_left, gparent);
213 if (tmp)
214 rb_set_parent_color(tmp, gparent, RB_BLACK);
215 __rb_rotate_set_parents(gparent, parent, root, RB_RED);
216 augment_rotate(gparent, parent);
217 break;
218 }
219 }
220 }
L.183以降は、親が祖父の右の子だった場合です。if節(L.116)と処理としては左右対称となります。コードを注意深く見てみると、コードをコピペして、「right」と「left」を相互変換しただけです。処理としても、それで正しいです。コメントもあっさりですね。説明も割愛します。
あとがき
かなりの分量になってしまったので、今回は一旦ここで区切ろうと思います。次回は、これの続きで、ノードの削除のアルゴリズムについて説明します。お楽しみに。
*1:vm_area_structの管理に使用しているとの記述があります。ちなみに、現在、vm_area_structの管理にはmaple treeというものが使われています。maple treeについては、機会があれば拾いましょう。